Bayesian Inference for Cosmology with JAX
Wassim Kabalan
Alexandre Boucaud, François Lanusse
2025-05-01


Outline for This Presentation
- Understand Cosmological Inference: Learn how we go from observations to cosmological parameters.
- From χ² to Bayesian Inference: See how Bayesian modeling generalizes classical approaches.
- Learn Forward Modeling and Hierarchical Models: Understand generative models and field-level inference.
- Explore Modern Tools (JAX, NumPyro, BlackJAX): Use practical libraries for scalable inference.
- Prepare for Hands-On Notebooks: Apply Bayesian techniques in real examples using JAX.
Background : Inference in Cosmology: The Big Picture
Inference in Cosmology: The Frequentist Pipeline
- cosmological parameters (Ω): matter density, dark energy, etc.
- Predict observables: CMB, galaxies, lensing
- Extract summary statistics: \(P(k)\), \(C_\ell\) , 2PCF
- Compute likelihood: \(L(\Omega \vert data)\)
- Estimate \(\hat{\Omega}\) via maximization (\(\chi^2\) fitting)
Frequentist Toolbox
- Optimizers/Gradient descent
- 2-point correlation function (2PCF)
- Power spectrum fitting: \(P(k)\), \(C_\ell\)
Inference in Cosmology: The Bayesian Pipeline
- Start from summary statistics: \(P(k)\), \(C_\ell\) , 2PCF
- Sample from a Prior \(P(\Omega)\)
- Compute likelihood: \(L(Obs \vert \Omega)\)
- Sampler from the Posterior \(P(\Omega \vert Obs)\)
Bayesian Toolbox
- Priors encode beliefs: \(P(\Omega)\)
- Hierarchical Bayesian Modeling (HBM)
- Probabilistic programming (e.g., NumPyro)
- Gradient-based samplers: HMC, NUTS
Inference in Cosmology: The Bayesian Pipeline
- Prior: Theory-driven assumptions \(P(\Omega)\)
- Latent variables: Hidden/unobserved \(z \sim P(z \mid \Omega)\)
- Likelihood: Generates observables \(P(\text{Obs} \mid \Omega, z)\)
- Posterior: infer \(P(\Omega \mid \text{Obs})\)
Inference in Cosmology: The Bayesian Pipeline
Bayes’ Rule with all components:
Full decomposition of the posterior. The denominator marginalizes over all possible parameters.
\[ \underbrace{P(\Omega \mid \text{Obs})}_{\text{Posterior}} = \frac{ \underbrace{P(\text{Obs} \mid \Omega)}_{\text{Likelihood}} \cdot \underbrace{P(\Omega)}_{\text{Prior}} }{ \underbrace{ \int P(\text{Obs} \mid \Omega) P(\Omega) \, d\Omega }_{\text{Evidence}} } \]
\[ \underbrace{P(\Omega \mid \text{Obs})}_{\text{Posterior}} = \frac{ \underbrace{\int P(\text{Obs} \mid \Omega, z)\, P(z \mid \Omega)\, dz}_{\text{Likelihood (marginalized over latent $z$)}} \cdot \underbrace{P(\Omega)}_{\text{Prior}} }{ \underbrace{ \int \left[ \int P(\text{Obs} \mid \Omega, z)\, P(z \mid \Omega)\, dz \right] P(\Omega)\, d\Omega }_{\text{Evidence}} } \]
In practice, we drop the evidence term when sampling — it’s a constant.
\[ P(\Omega \mid \text{Obs}) \propto \underbrace{\int P(\text{Obs} \mid \Omega, z)\, P(z \mid \Omega) \, dz}_{\text{Marginal Likelihood}} \cdot \underbrace{P(\Omega)}_{\text{Prior}} \]
\[ \log P(\Omega \mid \text{Obs}) = \log P(\text{Obs} \mid \Omega) + \log P(\Omega) \]
Bayes’ Rule in Practice
The posterior combines theory (prior) and data (likelihood) to infer cosmological parameters.
Latent variables \(z\) encode hidden structure (e.g., initial fields, nuisance parameters).
The evidence is often ignored during sampling (it’s constant).
Model comparison via the Bayes Factor:
\[ \text{Bayes Factor} = \frac{P(\text{Obs} \mid \mathcal{M}_1)}{P(\text{Obs} \mid \mathcal{M}_2)} \]
Two Roads to Inference: Frequentist and Bayesian

Conceptual Differences
| Concept | Frequentist | Bayesian |
|---|---|---|
| Parameters | Fixed but unknown | Random variables with a prior |
| Goal | Point estimate (e.g. MLE) | Full distribution (posterior over parameters) |
| Uncertainty | From data variability | From parameter uncertainty (posterior) |
| Prior Knowledge | Not used | Explicitly included via prior \(P(\Omega)\) |
| Interval Meaning | Confidence interval: “95% of experiments contain truth” | Credible interval: “95% chance truth is in this range” |
| Likelihood Role | Central in \(\chi^2\) minimization, fits | Combined with prior to form posterior |
| Inference Output | Best-fit estimate + error bars | Posterior distribution |
| Tooling | Optimization (e.g. χ², maximum likelihood) | Sampling (e.g. MCMC, HMC, NUTS) |
Although these approaches are often contrasted, they’re not mutually exclusive. Modern workflows — like causal inference in Statistical Rethinking — draw on both perspectives. Bayesian methods offer a formal way to combine theory and data, especially powerful when simulations are involved.
🛠️ The Mechanics of Inference
Sampling the Posterior: The Core Loop
The Sampling Loop:
- Start from a sample \((\Omega^t, z^t)\)
- Propose new sample \((\Omega', z')\)
- Compute acceptance probability
- Accept or reject proposal
- Repeat and store accepted samples ⟶ posterior
Goal: Explore the full shape of the posterior
(even in high-dim, non-Gaussian spaces)
Key Takeaways
- Most samplers follow this accept/reject loop
- Differ by how they propose samples: – Random walk (e.g., MH) – Gradient-guided (e.g., HMC, NUTS)
- Some skip rejection (e.g., Langevin, VI)
Sampling Algorithms at a Glance
Metropolis-Hastings (MCMC)
Propose: Random walk \(\Omega' \sim \mathcal{N}(\Omega^t, \sigma^2)\)
Accept:
\[ \alpha = \min\left(1, \frac{P(\text{Obs} \mid \Omega') P(\Omega')}{P(\text{Obs} \mid \Omega^t) P(\Omega^t)}\right) \]
Hamiltonian Monte Carlo (HMC)
- Propose: Simulate physics Trajectory via gradients \(\nabla\_\Omega \log P(\text{Obs} \mid \Omega)\)
- Accept: Based on Hamiltonian energy conservation. \(\alpha = \min(1, e^{\mathcal{H}(\Omega^t, p^t) - \mathcal{H}(\Omega', p')})\)
NUTS (No-U-Turn Sampler) Same as HMC, but auto-tunes:
- Step size
- Trajectory length (stops before looping back)
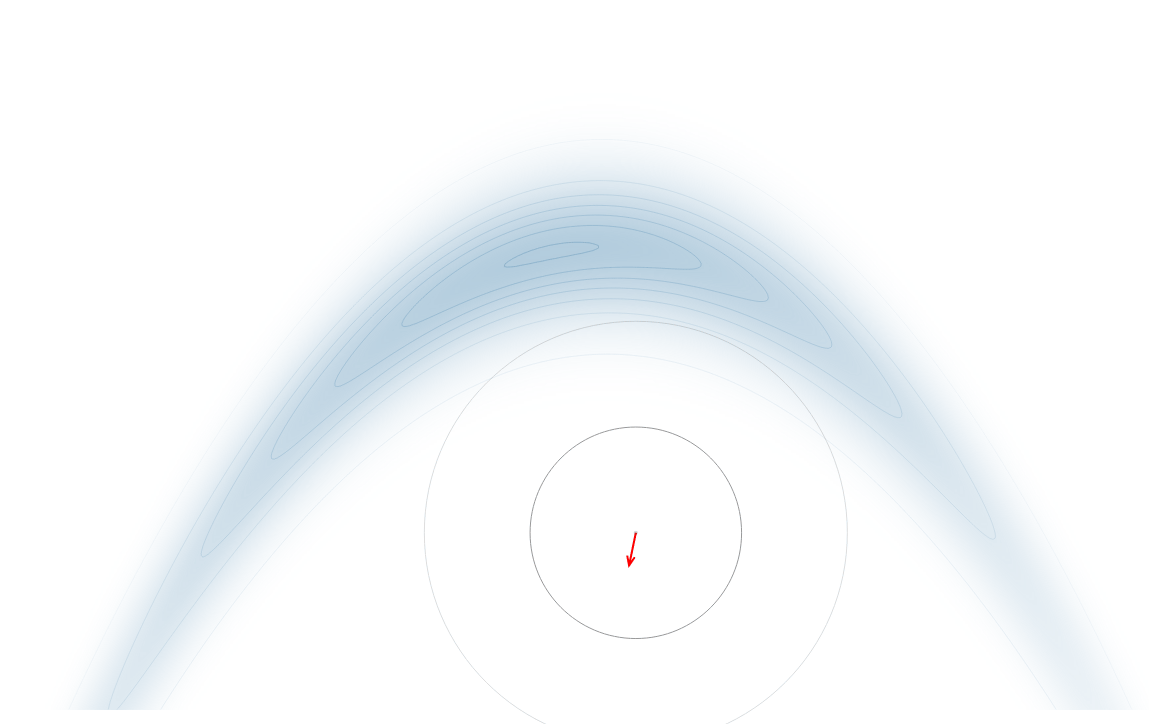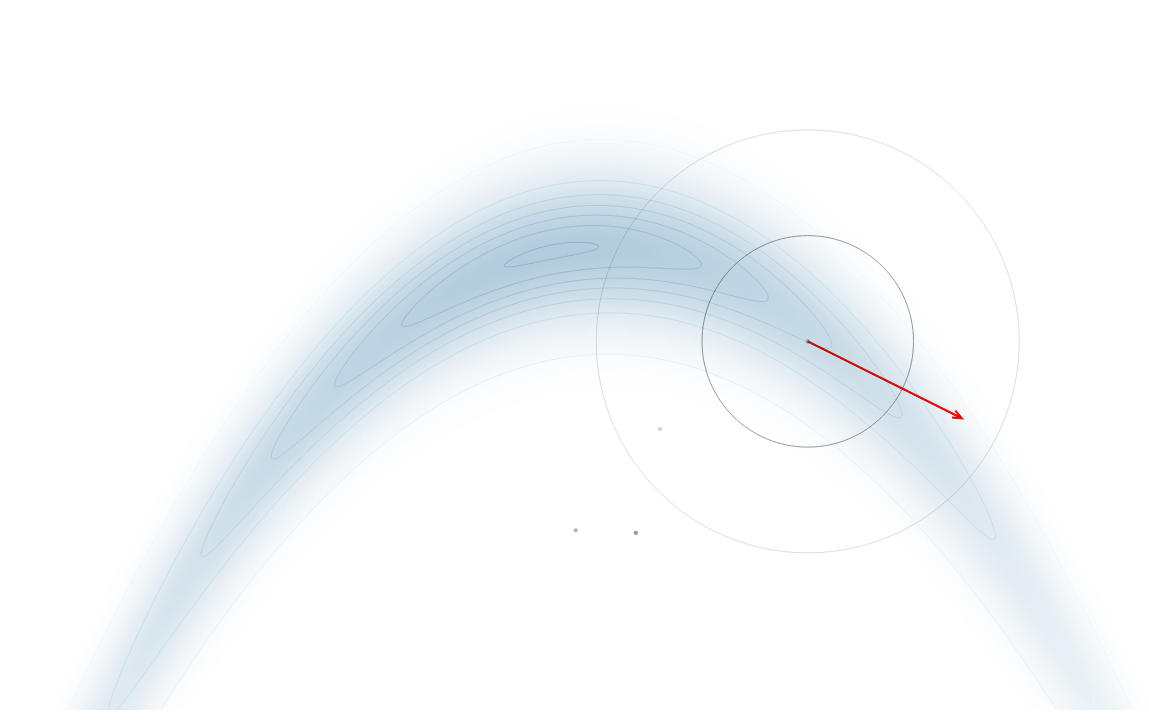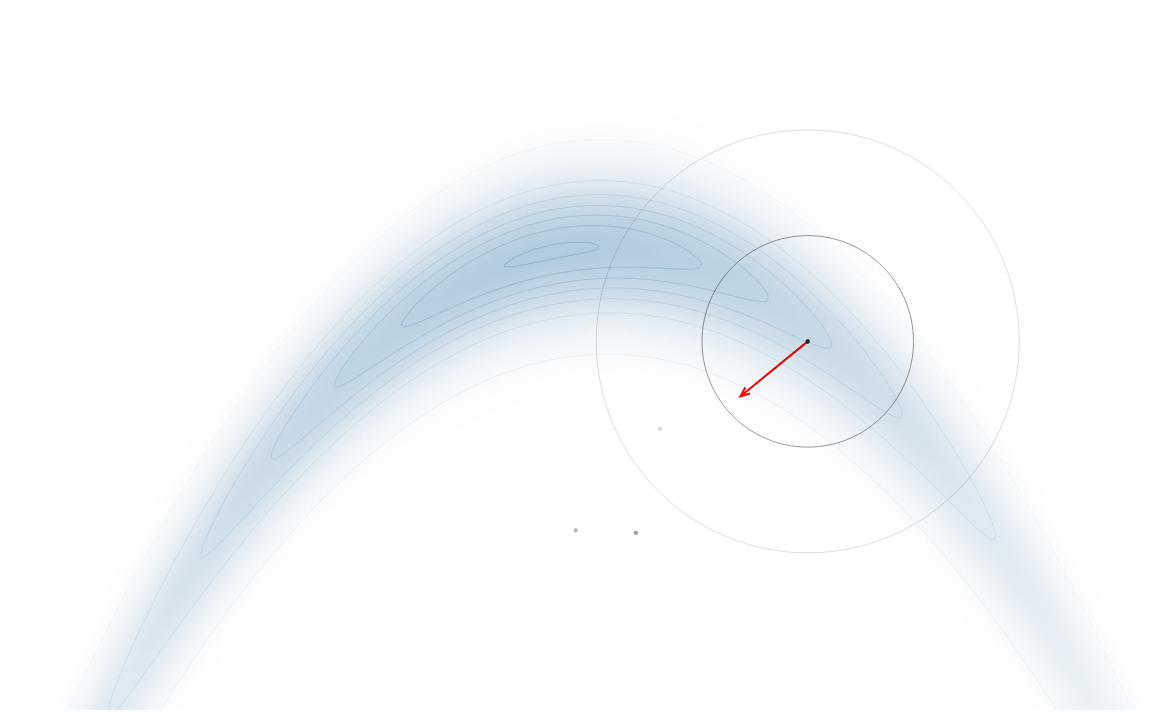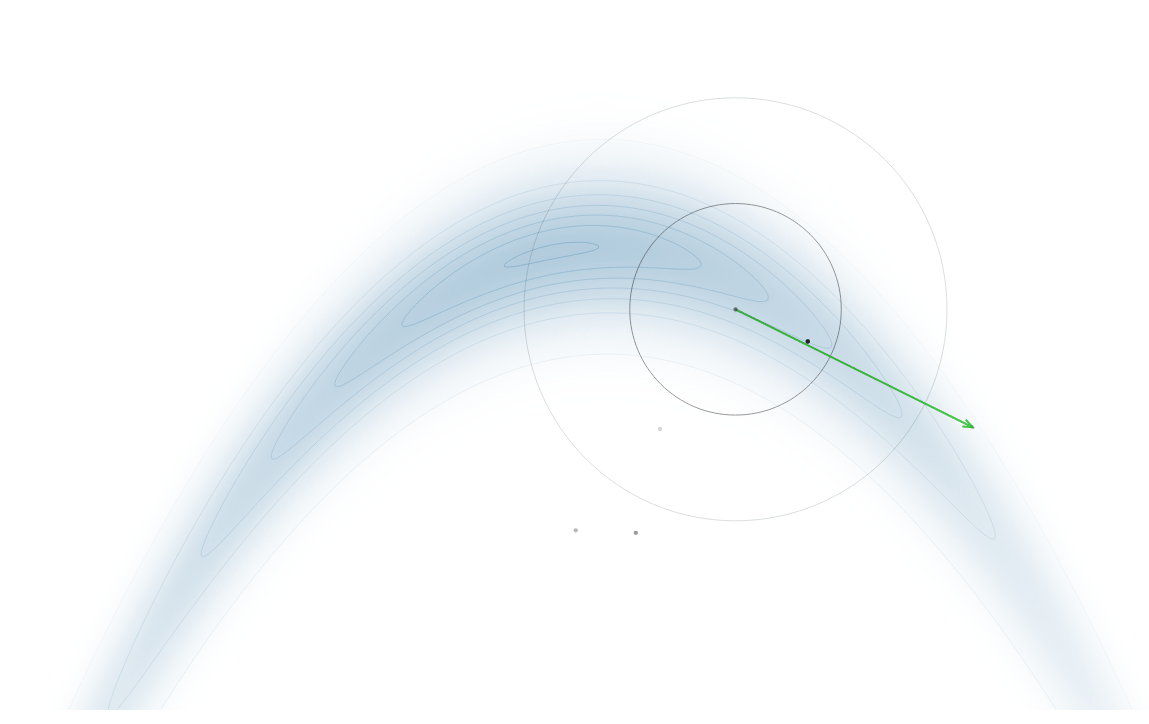
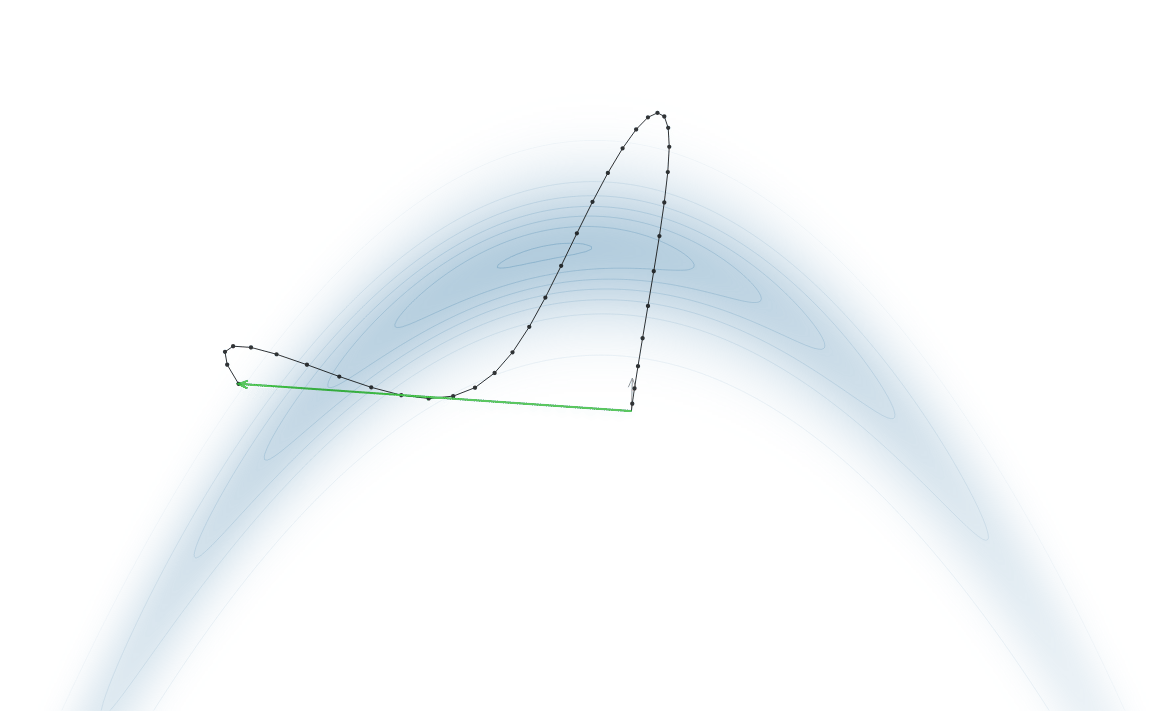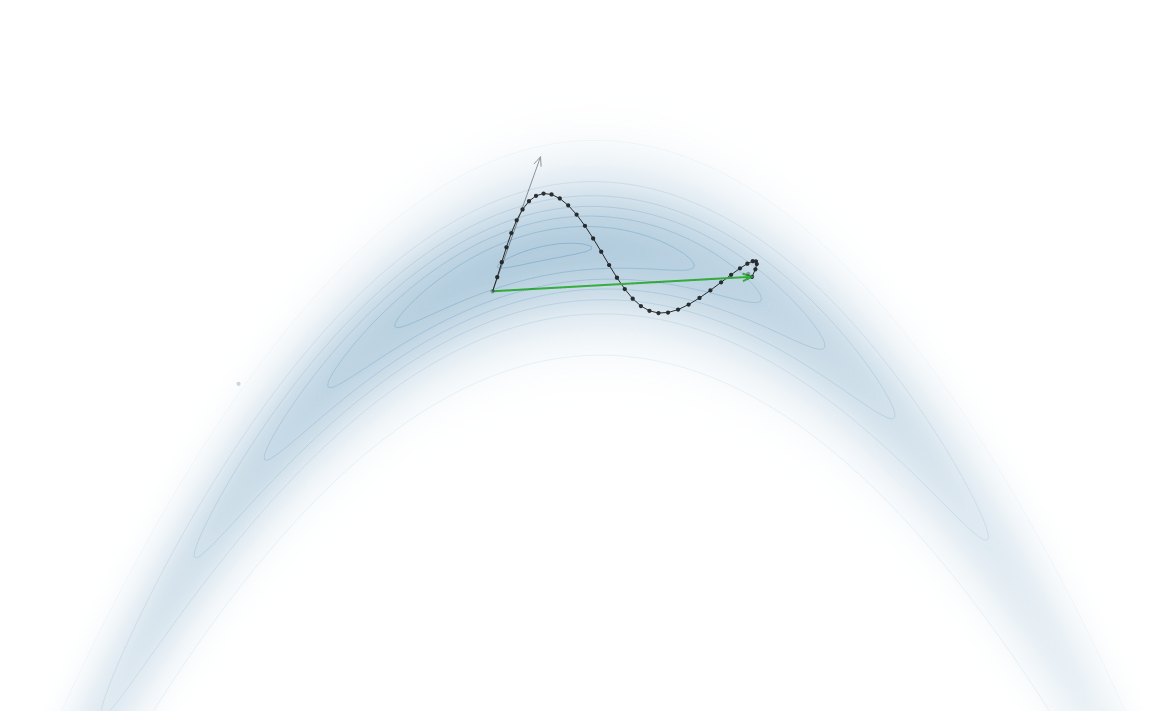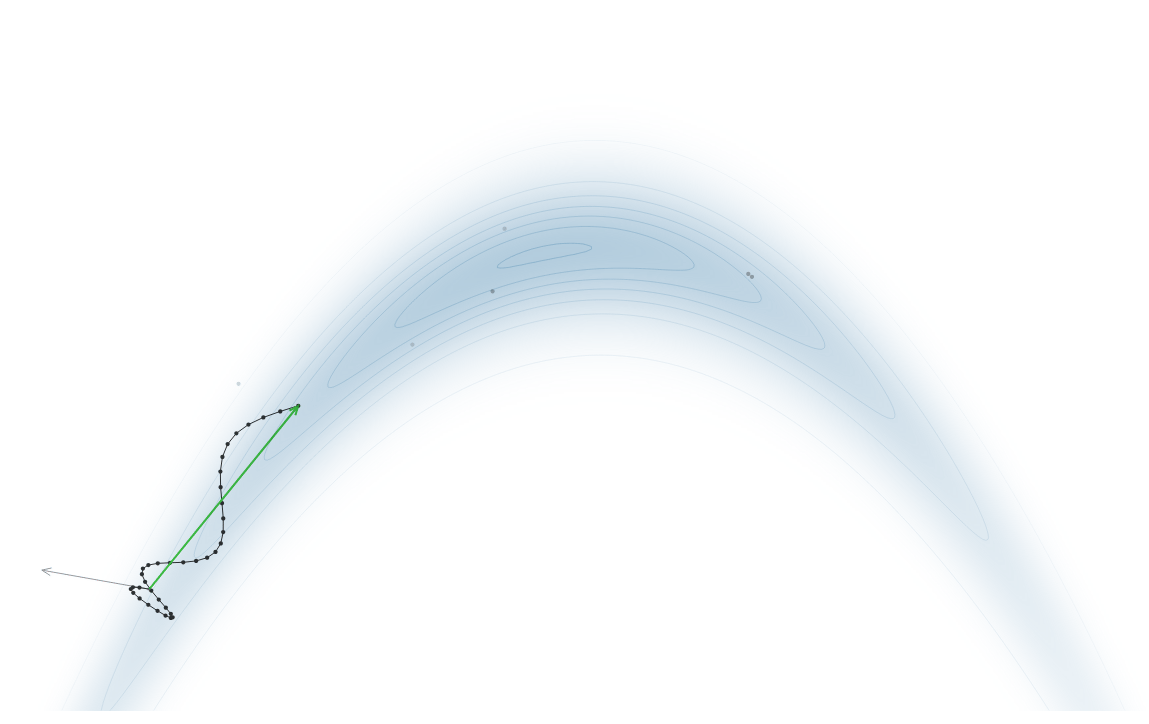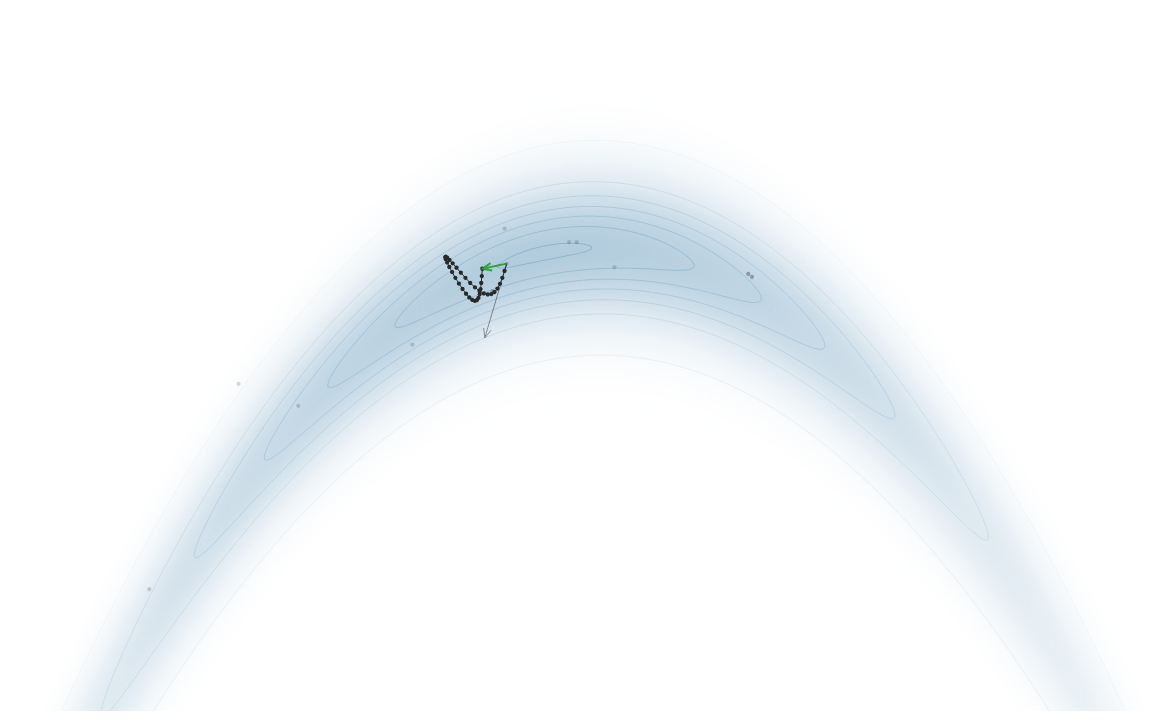

Gradient-Based Sampling in Action
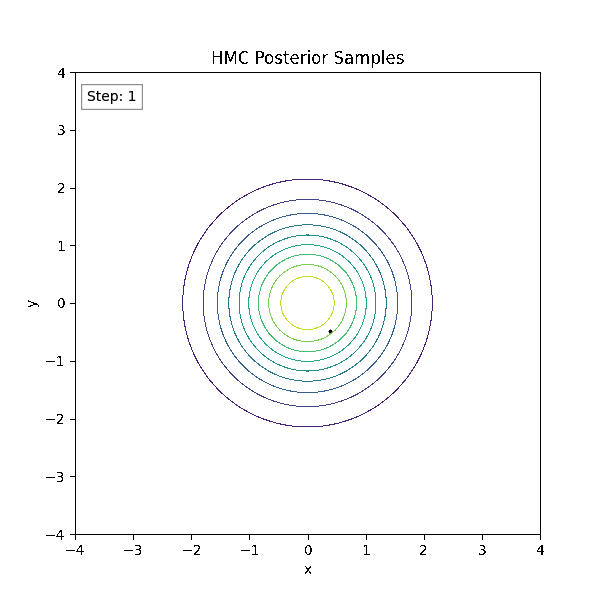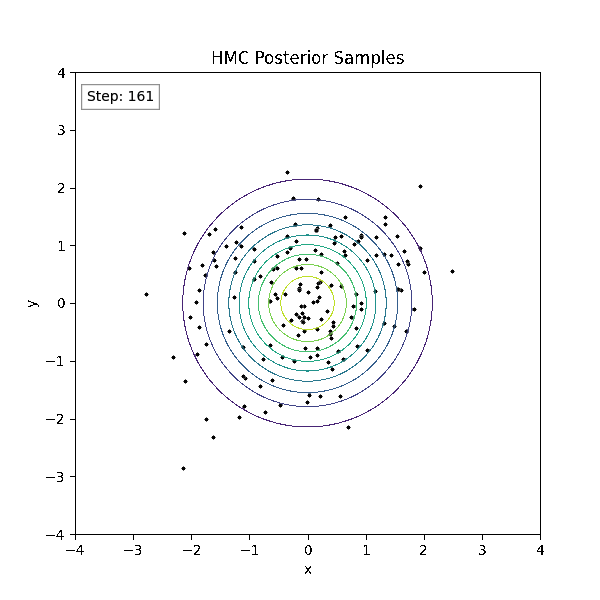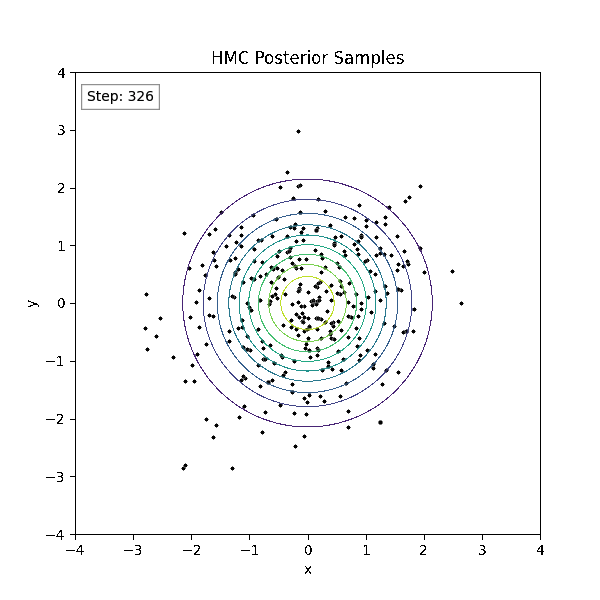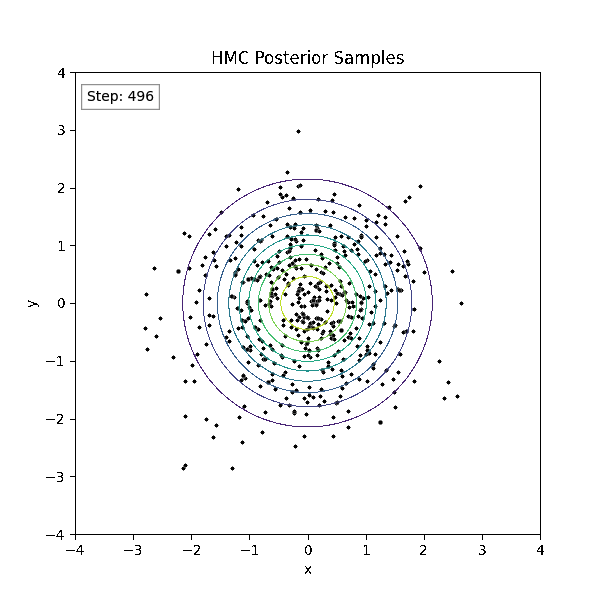
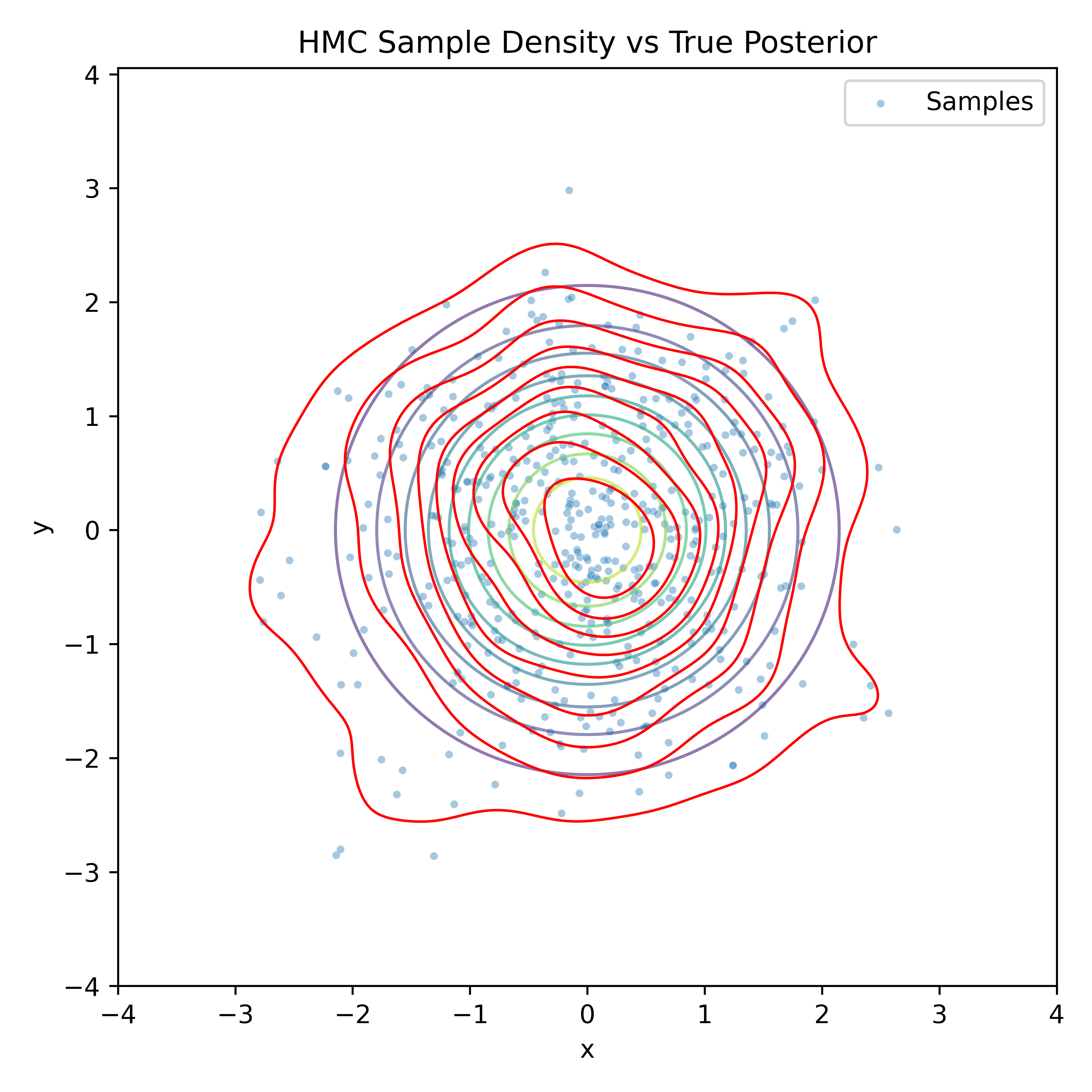

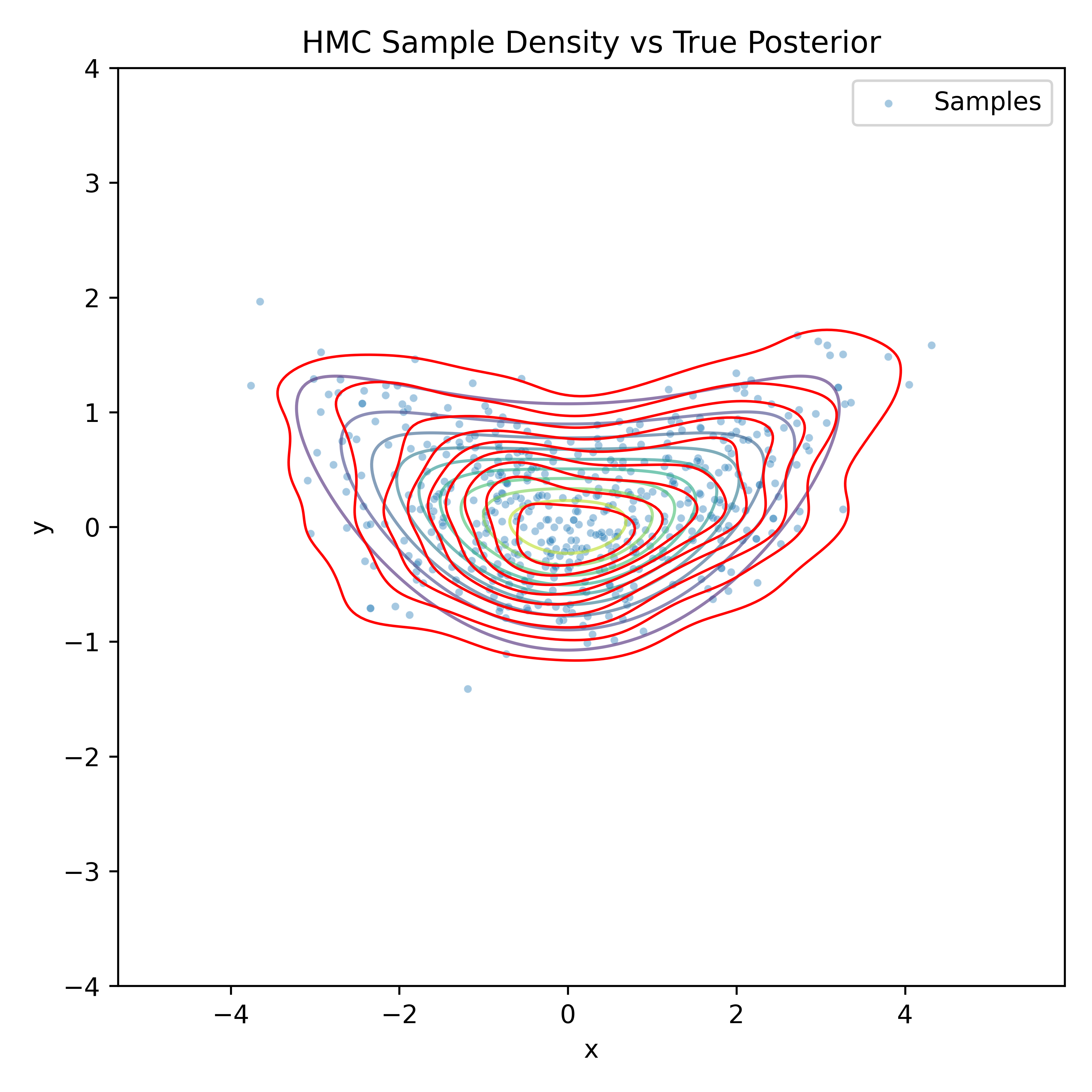
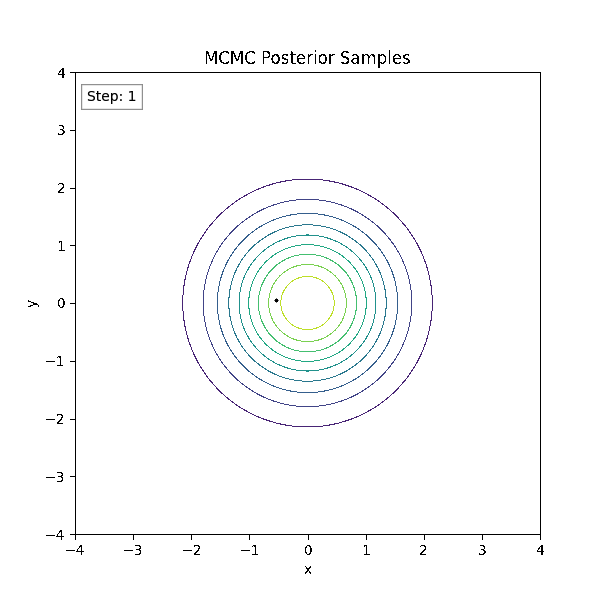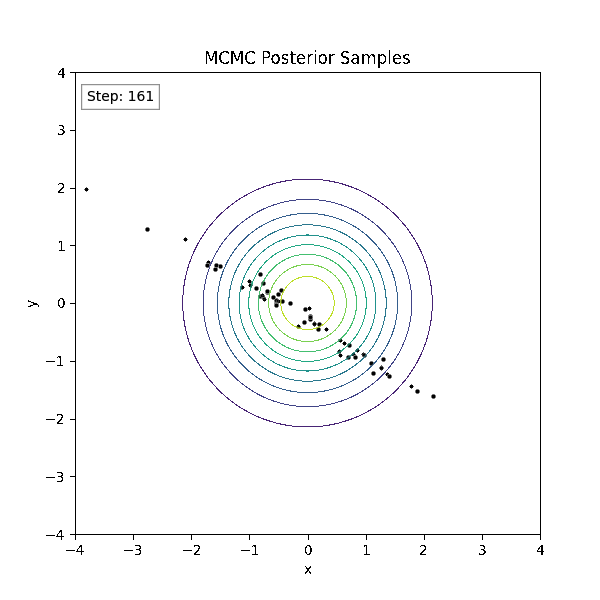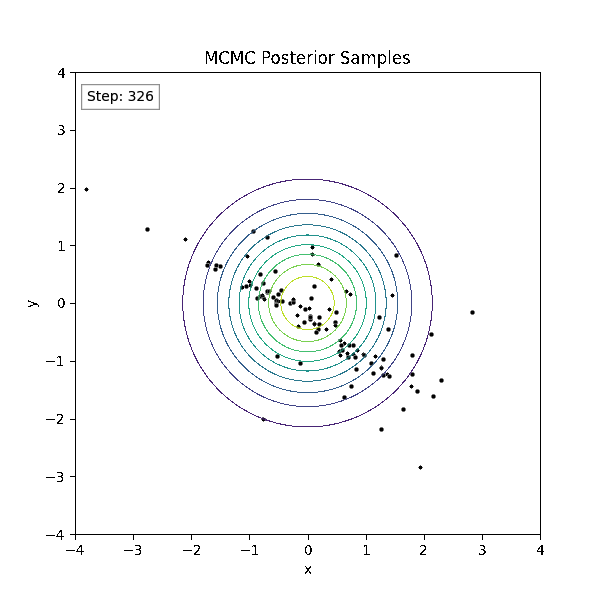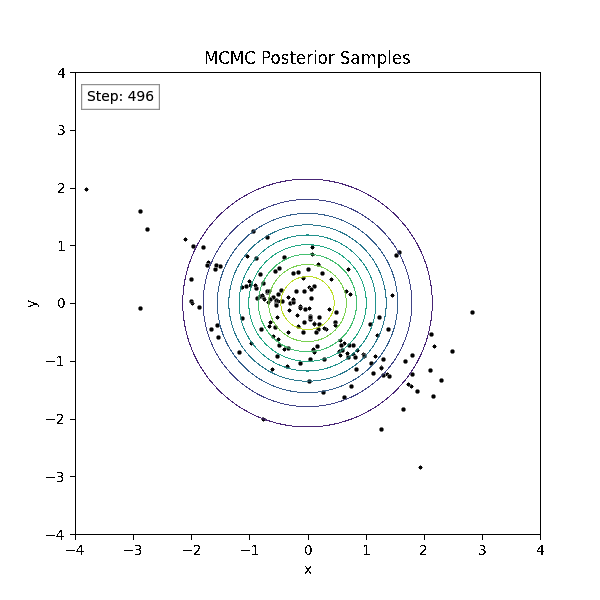
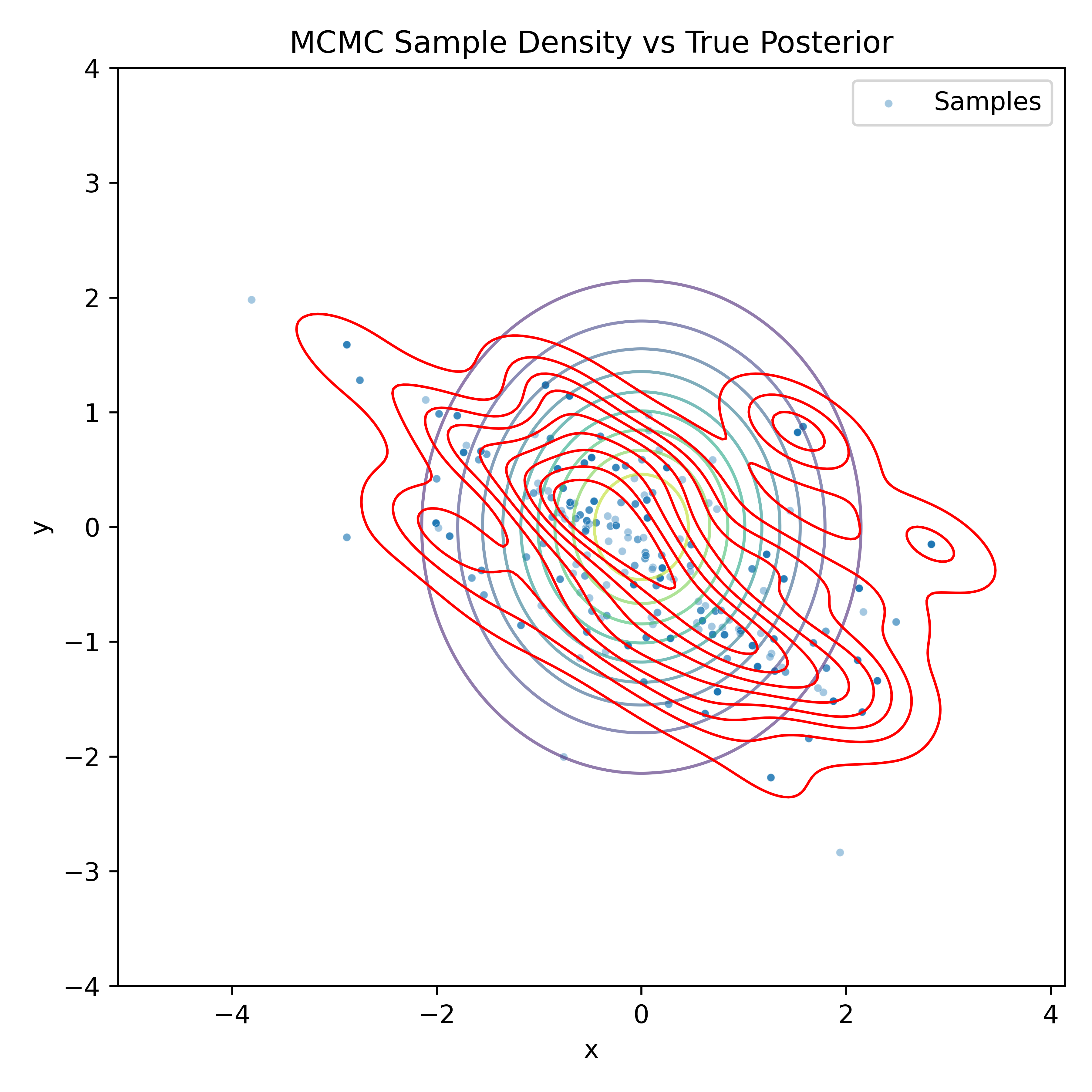


Gradient-Based Sampling in Action




- In high dimensions, random walk proposals (MCMC) often land in low-probability regions ⟶ low acceptance.
- To maintain acceptance, step size must shrink like \(1/\sqrt{d}\) ⟶ very slow exploration.
- HMC uses gradients to follow high-probability paths ⟶ better samples, fewer steps.

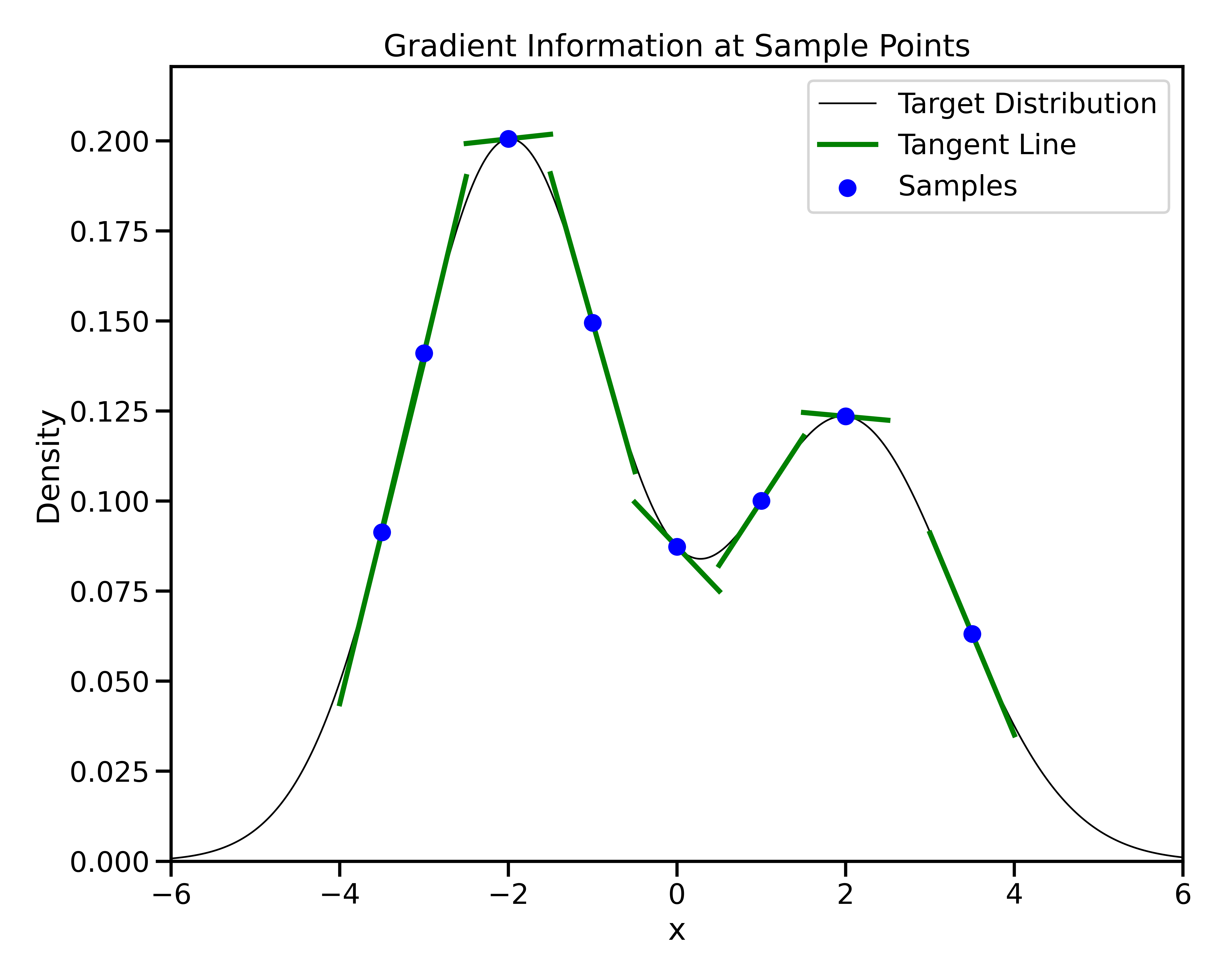
Differentiable Inference with JAX
When it comes to gradients, always think of JAX.
An Easy pythonic API
Easily accessible gradients using GRAD

Practical Bayesian Modeling & Inference with JAX
A Recipe for Bayesian Inference
1. Probabilistic Programming Language (PPL) NumPyro:
2. Computing Likelihoods JAX-Cosmo:
3. Sampling the Posterior NumPyro & Blackjax:
A Minimal Bayesian Linear Model
Define a simple linear model:
true_w = 2.0
true_b = -1.0
num_points = 100
rng_key = jax.random.PRNGKey(0)
x_data = jnp.linspace(-3, 3, num_points)
noise = jax.random.normal(rng_key, shape=(num_points,)) * 0.3
y_data = true_w * x_data + true_b + noise
def linear_regression(x, y=None):
w = numpyro.sample("w", dist.Normal(1., 2.))
b = numpyro.sample("b", dist.Normal(0., 2.)) # Fixed the second parameter
sigma = numpyro.sample("sigma", dist.Exponential(1.0))
mean = w * x + b
numpyro.sample("obs", dist.Normal(mean, sigma), obs=y)Run the model using NUTS:
Numpyro: Tips & Tricks for Bayesian Modeling
numpyro.handlers.seed: Fix randomness for reproducibility
numpyro.handlers.trace: Inspect internal execution and sample sites
numpyro.handlers.condition: Clamp a variable to observed or fixed value
numpyro.handlers.substitute: Replace variables with fixed values (e.g., MAP estimates)
numpyro.handlers.reparam: Reparameterize a site to improve geometry
Using BlackJax and NumPyro
BlackJax is NOT a PPL, so you need to combine it with a PPL like NumPyro or PyMC.
Initialize model and extract the log-probability function
Run warm-up to adapt step size and mass matrix using BlackJAX’s window adaptation
Run BlackJAX NUTS sampling using lax.scan
def run_blackjax_sampling(rng_key, state, kernel, num_samples=1000):
def one_step(state, key):
state, info = kernel(key, state)
return state, state
keys = jax.random.split(rng_key, num_samples)
_, samples = jax.lax.scan(one_step, state, keys)
return samples
samples = run_blackjax_sampling(rng_key, last_state, kernel)Sampler Comparison Table
| Sampler | Library | Uses Gradient | Auto-Tuning | Rejection | Best For | Notes |
|---|---|---|---|---|---|---|
| MCMC (SA) | NumPyro | ❌ | ❌ | ✅ | Simple low-dim models | No gradients; slow mixing |
| HMC | NumPyro / BlackJAX | ✅ | ❌ | ✅ | High-dim continuous posteriors | Needs tuned step size & trajectory |
| NUTS | NumPyro / BlackJAX | ✅ | ✅ | ✅ | General-purpose inference | Adaptive HMC |
| MALA | BlackJAX | ✅ | ❌ | ✅ | Local proposals w/ gradients | Stochastic gradient steps |
| MCLMC | BlackJAX | ✅ | ✅ (via L) | ❌ | Large latent spaces | Unadjusted Langevin dynamics |
| Adj. MCLMC | BlackJAX | ✅ | Manual (L) | ✅ | Bias-controlled Langevin sampler | Includes MH step |
For more information check Simons et al. (2025), §2.2.3, arXiv:2504.20130
Examples: Bayesian Inference for Cosmology
Power Spectrum Inference with jax-cosmo
Step 1: Simulate Cosmological Data
Define a fiducial cosmology to generate synthetic observations
Set up two redshift bins for galaxy populations
Define observational probes: weak lensing and number counts
Generate synthetic data using the fiducial cosmology
Step 2: Define the NumPyro Model
# Define a NumPyro probabilistic model to infer cosmological parameters
def model(data):
Omega_c = numpyro.sample("Omega_c", dist.Uniform(0.1, 0.5))
sigma8 = numpyro.sample("sigma8", dist.Uniform(0.6, 1.0))
# Forward model: compute theoretical prediction given parameters
cosmo = jc.Planck15(Omega_c=Omega_c, sigma8=sigma8)
mu, cov = jc.angular_cl.gaussian_cl_covariance_and_mean(cosmo, ell, probes)
# Likelihood: multivariate Gaussian over angular power spectra
numpyro.sample("obs", dist.MultivariateNormal(mu, cov), obs=data)Full Field Inference with Forward Models
Bayesian Inference using power spectrum data:
Bayesian Inference using full field data:
- Recap: Bayesian inference maps theory + data → posterior
- Cosmological Forward models
- Start from cosmological + latent parameters
- Sample initial conditions
- Evolve using N-body simulations
- Predict convergence maps in tomographic bins
- Simulation-Based Inference
- Compare predictions to real survey maps
- Build a likelihood from the forward model
- Infer cosmological parameters from full field data
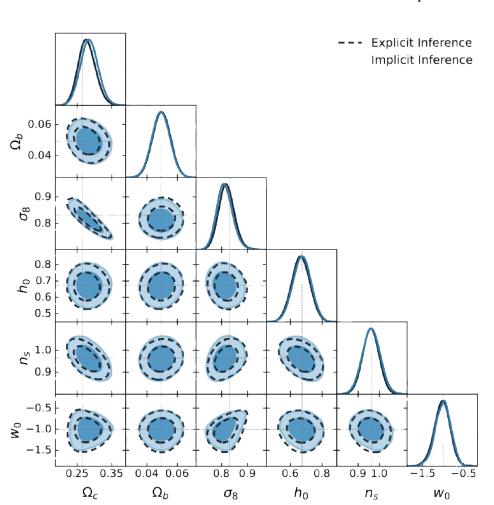
Full Field vs. Summary Statistics
- Preserves non-Gaussian structure lost in summaries
- Enables tighter constraints in nonlinear regimes
- Especially useful in high-dimensional inference problems
- See: Zeghal et al. (2024), Leclercq et al. (2021)
- 🔜 a talk on this topic this Thursday
Conclusion
Conclusion: Why Bayesian Inference?
Key Takeaways
Bayesian modeling enables flexible, end-to-end inference pipelines — from analytical likelihoods to full forward simulations.
The JAX ecosystem (NumPyro, BlackJAX, jax-cosmo…) lets you focus on modeling, not low-level math.
Gradients + differentiable simulators make inference scalable — even in complex, high-dimensional models.
These tools are now mature, fast, and usable — and already applied to realistic cosmological settings.
Future Work
Distributed, differentiable N-body simulations enable full-field inference at survey scale.
We look forward to applying these models to real survey data in upcoming projects.
Thank you for your attention!
Hands on notebooks
Bayesian Deep Learning Workshop , 2025